Mathematicians have described1 a brand new class of form that characterizes varieties generally present in nature — from the chambers within the iconic spiral shell of the nautilus to the best way wherein seeds pack into vegetation.
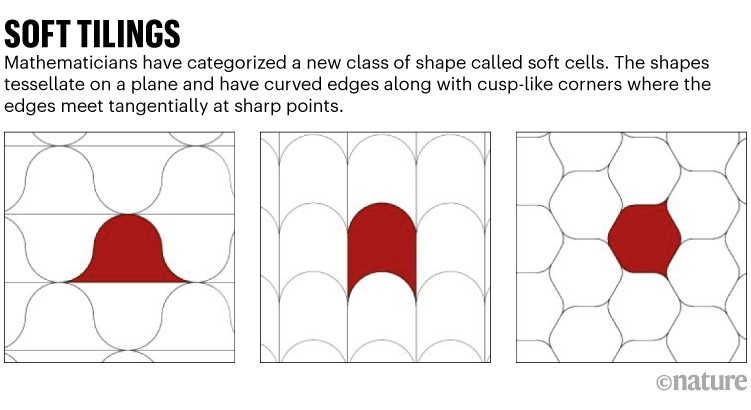
The work considers the mathematical idea of ‘tiling’: how shapes tessellate on a floor. The issue of filling a aircraft with an identical tiles has been so totally explored since antiquity that it’s tempting to suppose that there’s nothing left to be found about it. However the researchers deduced the ideas of tilings with a brand new set of geometric constructing blocks which have rounded corners, which they time period ‘tender cells’.
‘Geometry may be quite simple, however completely deep’: meet high maths prizewinner Claire Voisin
“Merely, nobody has finished this earlier than”, says Chaim Goodman-Strauss, a mathematician on the Nationwide Museum of Arithmetic in New York Metropolis, who was not concerned within the work. “It’s actually wonderful what number of basic items there are to think about.”
It has been recognized for millennia that solely sure forms of polygonal tile, akin to squares or hexagons, may be packed collectively to fill 2D area with no gaps. Tilings that fill area with no repeatedly repeating association, akin to Penrose tilings, have attracted curiosity for the reason that discovery of non-periodic buildings referred to as quasicrystals within the Eighties. Final yr, the primary quasiperiodic tiling, missing any true periodicity, that makes use of only a single tile form was introduced by Goodman-Strauss and his colleagues2.
Supply: Ref. 1
Avoiding corners
Mathematician Gábor Domokos on the Budapest College of Know-how and Economics and his co-workers returned to periodic polygonal tilings — however thought-about what occurs when a few of the corners are rounded. In two dimensions, not all corners may be rounded with out leaving gaps. However space-filling tilings turn out to be potential when some corners are deformed into ‘cusp shapes’. These corners have inside angles of zero — their edges meet tangentially as in a teardrop, and so they match snugly subsequent to the rounded corners (see ‘Mushy tilings’).
Domokos and colleagues devised an algorithm for easily changing geometric tiles — both 2D polygons or 3D polyhedra, just like the bubbles of a foam — into tender cells, and explored the vary of potential shapes these guidelines allow. In 2D, the choices are pretty restricted: all tiles should have at the very least two cusp-like corners. However in 3D, introducing softness has some surprises in retailer. Particularly, these tender cells can fill volumetric area with out having any corners in any respect.
The researchers devised a quantitative measure of the diploma of ‘softness’ of such space-filling 3D tiles, and located that the softest aren’t compact shapes, however as a substitute develop flange-like round ‘wings’ at their edges, usually rising from saddle-like tile surfaces. The softest form components are in truth round discs, which the flanges of the 3D tiles approximate.
The price of kinks
Domokos thinks that, for any given preliminary polyhedral tiling, there’s a distinctive tiling with the best potential softness. He additionally suspects that, in actual supplies, this optimum will end up to maximise some bodily amount associated to, say, the bending power within the edges or the interfacial pressure. He admits that he and his colleagues at the moment haven’t any proof of this maximal-softness conjecture, however hopes “that somebody a lot smarter will decide this up and show it”.
Supply: Ref. 1
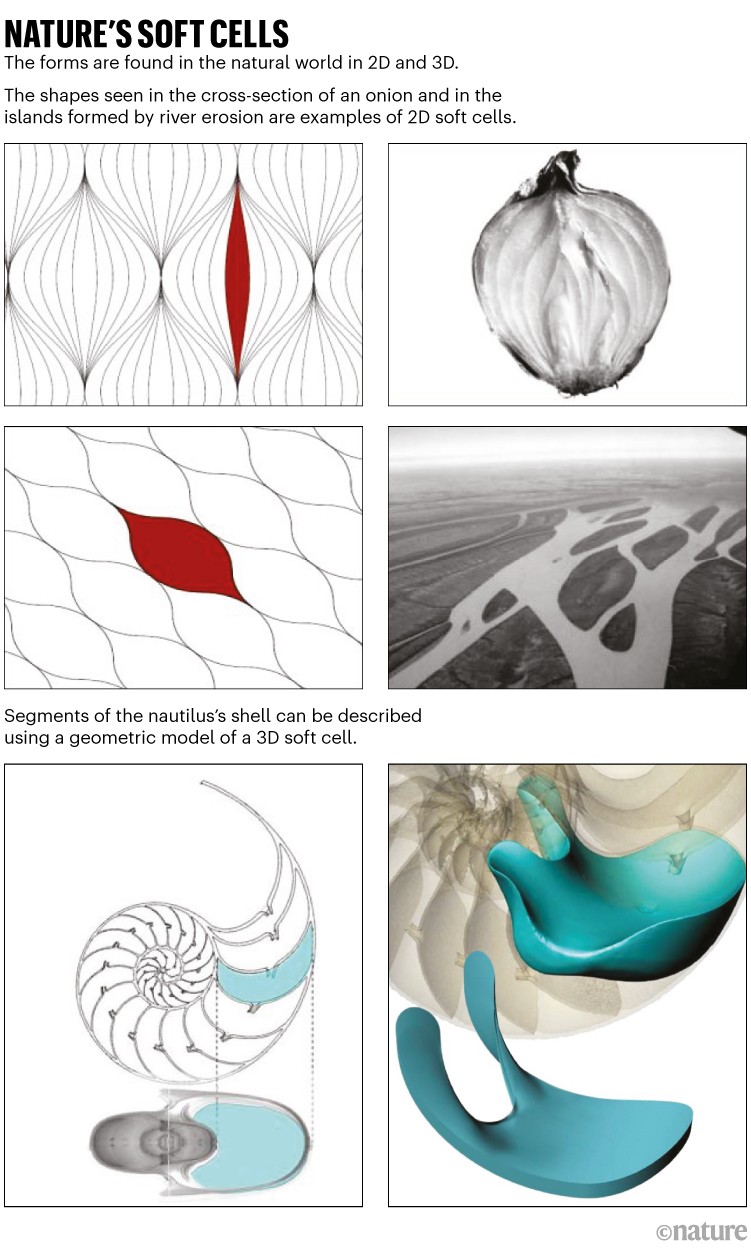
The researchers recognized tender tilings in nature within the 2D shapes of islands in braided rivers, cross-sections of the concentric layers in an onion and organic cells in a tissue, in addition to the 3D compartments of spiral shells akin to these of the nautilus, a marine mollusc (see ‘Nature’s tender cells’). Nature typically seeks to keep away from corners, they suppose, as a result of such kinks have a excessive price in deformation power and may be sources of structural weak spot.
Learning the nautilus “was the turning level” of the work, says Domokos. In cross-section, the shell compartments appeared like 2D tender cells with two corners. However co-author Krisztina Regős, additionally on the Budapest College of Know-how and Economics, suspected that the precise 3D chamber had no corners in any respect. “That sounded unbelievable,” says Domokos. “However later we discovered that she was proper.”
Historical geometry
On condition that the evaluation makes use of arithmetic that has been recognized for hundreds of years, it may appear stunning that nobody has formalized the notion of sentimental cells till now. However Goodman-Strauss suspects that “the tender edges are sufficient of a block for geometers to not have thought of it” beforehand.
“The universe of polygonal and polyhedral tilings is so fascinating and wealthy that mathematicians didn’t have to develop their playground,” says Domokos. He suspects that there’s a widespread notion that recent insights demand superior arithmetic or cutting-edge computation, not merely well-established geometric strategies.

The Heydar Aliyev Middle in Baku was designed architect Zaha Hadid, whose buildings use tender cells to keep away from or decrease corners.Credit score: Mladen Antonov/AFP through Getty
Goodman-Strauss sees the work as providing “a sort of descriptive language of construction”, however which could not but reveal new bodily ideas underlying the formation of such buildings in nature. To know, say, river banks, he says, it’s in all probability nonetheless needed to think about the bodily course of from first ideas, such because the roles of stream, sediment transport and erosion.
Domokos and colleagues suppose that architects akin to Zaha Hadid have lengthy used tender cells intuitively to keep away from or decrease corners, both for aesthetic or structural causes. Since finishing the paper, Domokos and co-author Alain Goriely of the College of Oxford, UK, have collaborated with architects on the California School of Arts in San Fransisco, who devised an award-winning construction utilizing soft-cell components made — appropriately — from eggshells.


